Grouped variable selection for generalized eigenvalue problems

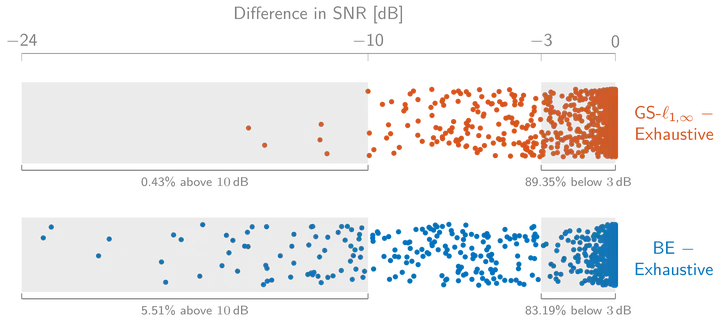
Many problems require the selection of a subset of variables from a full set of optimization variables. The computational complexity of an exhaustive search over all possible subsets of variables is, however, prohibitively expensive, necessitating more efficient but potentially suboptimal search strategies. We focus on sparse variable selection for generalized Rayleigh quotient optimization and generalized eigenvalue problems. Such problems often arise in the signal processing field, e.g., in the design of optimal data-driven filters. We extend and generalize existing work on convex optimization-based variable selection using semidefinite relaxations toward group-sparse variable selection using the l_1,infinity-norm. This group-sparsity allows, for instance, to perform sensor selection for spatio-temporal (instead of purely spatial) filters, and to select variables based on multiple generalized eigenvectors instead of only the dominant one. Furthermore, we extensively compare our method to state-of-the-art methods for sensor selection for spatio-temporal filter design in a simulated sensor network setting. The results show both the proposed algorithm and backward greedy selection method best approximate the exhaustive solution. However, the backward greedy selection has more specific failure cases, in particular for ill-conditioned covariance matrices. As such, the proposed algorithm is the most robust currently available method for group-sparse variable selection in generalized eigenvalue problems.